LDA는 임의의 문서를 K개의 토픽 분포로 표현하고, 각 토픽은 V개의 단어 분포로 표현하는 모델이다.

토픽 갯수 K와 단어집 갯수 V는 하이퍼파라미터이다. 특히 토픽 갯수 K를 지정하지 않는, 좀 더 advanced한 방법론도 존재하는데 Hierarchical Dirichlet Process에서 소개하도록 하겠다.

일반적으로 사람들이 글을 쓸 때는 여러가지 소재를 담아 이야기를 구성한다. 이때 이 소재가 바로 토픽모델에서 말하는 토픽(Topic) 이다.

예를들어, 신문 기자가 "애플, 아이폰 출시" 라는 제목으로 기사를 작성한다고 가정해보자. 보통 이런 기사에는 아이폰, iOS, 카메라 등 제품 혹은 기술에 대한 소재, 그리고 생산량, 수요, 판매, 실적 등 어떤 시장 상황과 관련된 소재 등 다양한 소재로 이야기가 구성된다.

이렇듯 LDA가 문서를 복수개 토픽의 mixture로 표현하고, 각 토픽을 각 토픽을 설명하는 복수개 단어의 mixture로 표한하는 것(mixture of mixture)은 상당히 자연스럽고 합리적인 것 이라고 볼 수 있다.

위 그림은 지금 까지 설명한 내용을 최대한 이해하기 쉽게 표현해 본 것인데, 이를 좀 더 formal하게 나타낸다면 다음과 같은 Graphical Model로 설명 할 수 있다.

Graphical Model

Graphical Model이란, 확률 모델을 표현하는 그래프로써 확률 변수(Random Variable)간의 상호 의존성을 나타내기 용이하고 주로 베이지안 통계에서 많이 사용된다.

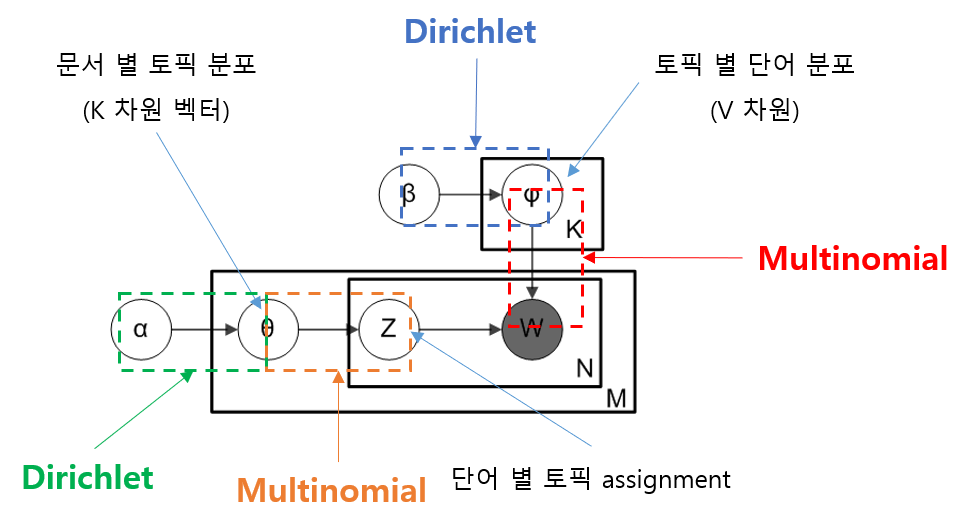
Graphical Model은 LDA 모델을 직관적으로 이해하는데 도움이 된다. 아래 그림과 같은 표현법을 plate notation이라고 하는데 동그라미는 확률 변수를, 화살표는 변수간 의존성을 의미한다. $W$ 동그라미는 특별히 까맣게 색칠되어 있는데 이것은 관측된 것이라는 의미이다.

LDA는 비지도 학습 모델(Unsupervised Model)로 모델 학습을 위해 주어지는 것은 텍스트 코퍼스, 즉 문서 내에 있는 단어들 뿐이다.

가장 큰 사각형은 문서를 의미하는데 전체 M개의 문서가 있다는 것이고 각 문서의 토픽 분포가 $\theta$라는 것을 의미한다. 이 내부에 있는 작은 사각형은 문서에 포함된 단어를 의미하는데 각 문서에는 N개의 단어가 있다는 뜻이고, 각 단어를 $W$로 표현하고 이 단어에 대응하는 토픽(assignment 혹은 indicator)은 $Z$로 표현하고 있다. 가장 작은 사각형은 K개의 토픽을 의미하는데, 각 토픽의 단어 분포를 $\phi$로 표현하고 있다.

• $M$: 전체 문서의 갯수
• $N$: 문서 내 단어 갯수 ($i$ 문서는 $N_i$ 단어를 가짐)
• $\alpha$: 문서 별 토픽 분포에 대한 사전 확률 분포(prior)인 디리클레 분포의 파라미터 ($K$ 차원 벡터)
• $\beta$: 토픽 별 단어 분포에 대한 사전 확률 분포(prior)인 디리클레 분포의 파라미터 ($V$ 차원 벡터)
• $\theta_i$: 문서 $i$의 토픽 분포 ($K$ 차원 벡터)
• $\phi_k$: 토픽 $k$의 단어 분포 ($V$ 차원 벡터)
• $z_{ij}$: $i$문서의 $j$번째 단어의 토픽
• $w_{ij}$: $i$문서의 $j$번째 단어

Graphical Model과 이어서 설명할 Generative Story를 통해서, LDA가 많은 수의 문서만 이용하여, 어떻게 텍스트의 시멘틱한 구조를 만들어 낼 수 있는지 가늠해 볼 수 있을 것이다.

Generative Story

임의의 문서는 첫번째 단어, 두번째 단어, 세번째 단어, ... 이렇게 한단어 한단어씩 씌여지는데, 각 단어는 어떤 토픽에 대한 멤버쉽을 갖는다.

다시말하면, 사람이 글을 쓸 때 단어를 하나를 선택하기에 앞서 어떤 토픽을 먼저 정하고, 그 토픽에 맞는 단어를 골라서 쓴다라고 생각을 해야한다. (이렇게 생각해야 LDA를 이해할 수 있다.) 이를 염두해 놓으면 아래에 있는 설명을 좀 더 쉽게 이해할 수 있다.

LDA에서는 문서의 발생 과정을 다음과 같이 가정 한다.

1. 사전 확률 분포인 디리클레 분포로부터 샘플링하여 $\theta_i$를 얻는다.
   • (그림 2의 초록색 점선)
   • $\theta_i \sim Dir(\alpha)$
   • 코퍼스에 총 $M$개의 문서가 있으므로 $\theta_1$, ..., $\theta_M$
2. 사전 확률 분포인 디리클레 분포로 부터 샘플링하여 $\phi_k$를 얻는다.
   • (그림 2의 파란색 점선)
   • $\phi_k \sim Dir(\beta)$
   • 토픽 갯수를 총 K개로 가정했으므로 $\phi_1$, ..., $\phi_K$
3. 문서 $i$의 각 단어가 선정되기 앞서 토픽이 선정되므로 $\theta_i$를 파라미터로 갖는 다항 분포로 부터 토픽 $z_{ij}$를 샘플링
   • (그림 2의 주황색 점선)
   • $z_{ij} \sim Multinomial(\theta_i)$
4. 토픽 $z_{ij}$가 선정되면 해당 토픽에서 $\phi_{z_{ij}}$를 파라미터로 갖는 다항 분포로 부터 단어 $w_{ij}$를 샘플링
   • (그림 2의 빨간색 점선)
   • $w_{ij} \sim Multinomial(\phi_{z_{ij}})$

문서의 토픽 분포, 토픽의 단어 분포 모두 다항 분포를 사용한다. 비유를 들어본다면, 문서가 작성된다는 것은 $K$개의 면이 있는 주사위를 던져 토픽을 뽑고, 뽑힌 토픽에 해당하는 ($V$개의 면이 있는) 다른 주사위를 던져, 단어를 뽑는 행위를 반복하는 것으로 본다.

LDA가 문서를 만들어 내는 것 처럼 어떤 확률적 생성 과정이 가능하려면, 앞서 설명한 주사위가 필요하다. 즉, 각 문서마다 토픽을 뽑을 수 있는 주사위가 필요하고 각 토픽마다 단어를 뽑을 수 있는 주사위가 필요하다. 이러한 주사위를 잘 깍아서 만드는 과정이 LDA를 학습하는 과정이라고 볼 수 있다.

베이지안 추론(Bayesian Inference)

LDA 모델에서, 소위 말해 학습이라고 하는 것은 관측할 수 있는 값인 $W$(단어)를 제외한 나머지를 모두 잠재 변수(Latent Variable)로 생각하고, 이에 대한 사후 확률 분포(Posterior Distribution)를 구하는 것을 말한다. (일단, 이 분포를 알아내는 과정을 베이지안 추론이라고 생각하면 된다.)

$$\begin{aligned} P(Z,\Theta,\Phi|W,\alpha,\beta) = \cfrac {P(W,Z,\Theta,\Phi;\alpha,\beta)} {P(W|\alpha,\beta)} \end{aligned}$$

여기서 우변의 분모는,

모든 문서-토픽 분포 $\Theta$, 모든 토픽-단어 분포 $\Phi$, 모든 토픽 assignments $Z$, 코퍼스의 모든 단어 $W$, 그리고 주어진 하이퍼파라미터 $\alpha$, $\beta$ 의 결합 확률 분포이다. 앞서 나왔던 Graphcial Model을 참조하여 아래와 같은 식으로 정리할 수 있다.

$$\begin{aligned} P(W,Z,\Theta,\Phi;\alpha,\beta) = \displaystyle\prod_{i=1}^{K} P(\phi_i;\beta)\displaystyle\prod_{j=1}^{M} \Bigg[ P(\theta_j;\alpha) \displaystyle\prod_{t=1}^{N} \bigg[ P(Z_{j,t} | \theta_j)P(W_{j,t}|\phi_{z_{jt}}) \bigg] \Bigg] \end{aligned}$$

그리고 우변의 분자는,

위 결합 확률 분포를 $\Phi$, $\Theta$, $Z$에 대하여 주변화(marginalize out) 함으로써 구할 수 있다. (이를 evidence 혹은 marginal likelihood라고 한다.)

$$\begin{aligned} P(W|\alpha,\beta) &= \displaystyle\int_{\Phi}\displaystyle\int_{\Theta}\displaystyle\sum_{Z}P(W,Z,\Theta,\Phi;\alpha,\beta)d\Theta d\Phi \\ &= \displaystyle\int_{\Phi} P(\Phi|\beta) \displaystyle\int_{\Theta} P(\Theta|\alpha) \displaystyle\sum_{Z} P(Z|\Theta)P(W|Z,\Phi) d\Theta d\Phi \end{aligned}$$

보통 현실 세계 문제에서, Evidence를 계산하는 것은 불가능한데 이를 보통 intractable하다고 표현한다. 왜냐하면 위 식에서 볼 수 있듯이, $\Theta$와 $\Phi$ 가 잠재 변수 Z에 대한 summation 내에 coupling 되어 있기 때문이다.

Z(topic assignment)에 대한 configuration이 $K^{|M*N|}$ 개 만큼 존재한다. 이처럼 베이지안 추론에서는 evidence의 존재가 LDA 같은 베이지안 모델을 어렵게 만드는 원인이라고도 볼 수 있다.

하지만, 이런 상황에도 해결 방법이 존재한다.

모델의 잠재 변수(엄밀하게는 파라미터)를 추정하기 위한 베이지안 추론에는 크게 두가지 방법론이 있다.

1. Variational Inference
2. Gibbs Sampling

베이지안 추론에 대해서는 다룰 내용이 방대하므로 별도의 페이지에서 정리를 할 예정이고, 여기에서는 Gibbs Sampling 방식으로 설명을 이어나가도록 하겠다.

(Collapsed) Gibbs Sampling

Gibbs Sampling은 intractable한 분포를 가진 사후 확률 분포(posterior)를 추론하는데 사용되는 일반적인 접근법이다.

LDA에서는 $\Phi$와 $\Theta$에 대한 사전 확률 분포(prior)가 conjugate하기 때문에, 결합 확률 분포로 부터 해당 확률 변수를 integrated out(=marginalized out)하여 계산하게 되는데, prior를 callapsing 한다고 하여 특별히 이것을 Collapsed Gibbs Sampling 이라고 부른다.

즉, Collapsed Gibbs Sampling의 목표는 아래와 같이 Z에 대한 사후 확률 분포를 구하는 것이다.

$$\begin{aligned} P(Z|W;\alpha,\beta) = \cfrac {P(Z,W;\alpha,\beta)} {P(W|\alpha,\beta)} \end{aligned}$$

먼저 위 식 4 우변의 분자는, 식 2 결합 확률 분포를 $\Phi$와 $\Theta$에 대하여 marginalize 하여 다음과 같이 정리해보자.

$$\begin{aligned} P(Z,W|\alpha,\beta) &= \displaystyle\int_{\Theta}\displaystyle\int_{\Phi}P(Z,W,\Theta,\Phi;\alpha,\beta)d\Phi d\Theta \\ &= \displaystyle\int_{\Phi}\displaystyle\prod_{i=1}^{K} P(\phi_i;\beta) \displaystyle\prod_{j=1}^{M} \displaystyle\prod_{t=1}^{N} P(W_{j,t}|\phi_{z_{jt}})d\Phi \cdot \displaystyle\int_{\Theta} \displaystyle\prod_{j=1}^{M} P(\theta_j;\alpha) \displaystyle\prod_{t=1}^{N} P(Z_{j,t} | \theta_j) d\theta \\ &= ... \\ &= \displaystyle\prod_{j=1}^{M} \cfrac {\Gamma \big(\sum_{i=1}^{K} \alpha_{i} \big)} {\prod_{i=1}^{K} \Gamma(\alpha_{i})} \cfrac {\prod_{i=1}^K \Gamma(n_{j,(\cdot)}^i)+\alpha_{i}} {\Gamma(\sum_{i=1}^{K} n_{j,(\cdot)}^{i} + \alpha_{i})} \times \displaystyle\prod_{i=1}^{K} \cfrac {\Gamma \big(\sum_{r=1}^{V} \beta_{r} \big)} {\prod_{r=1}^{V} \Gamma(\beta_{r})} \cfrac {\prod_{r=1}^V \Gamma(n_{(\cdot), r}^i)+\beta_{r}} {\Gamma(\sum_{r=1}^{V} n_{(\cdot),r}^{i} + \beta_{r})} \end{aligned}$$

• $n_{j,r}^{i}$: $j$번째 문서에서 vocabulary상 id값이 $r$인 단어에, id값이 i인 토픽이 할당된 단어(토큰)의 갯수
• $n_{j,(\cdot)}^{i}$: $j$번째 문서에서, id값이 i인 토픽이 할당된 단어(토큰)의 총 갯수

위 생략된 부분은 위키피디아에 디테일한 과정이 있으니 참고하기 바란다.

Gibbs Sampling은 사후 확률 분포를 직접 구하는 것이 아니라, 사후 확률 분포의 샘플(Z의 샘플)을 만들어 내는 것이 목표이기 때문에, Z에 대해서 불변한 값인 $P(W,\alpha,\beta)$를 무시하고, $P(Z,W,\Theta,\Phi;\alpha,\beta)$로부터 직접 Sampling Equation을 유도해 낼 수 있다.

Sampling Equation

$$\begin{aligned} P(Z_{(m,n)}|Z_{-(m,n)},W;\alpha,\beta) = \cfrac {P(Z_{(m,n)}, Z_{-(m,n)},W,\alpha,\beta)} {P(Z_{-(m,n)}, W|\alpha,\beta)} \end{aligned}$$

• $Z_{(m,n)}$: $m$번째 문서의 $n$번째 단어에 대한 토픽을 나타내는 확률 변수
• $Z_{-(m,n)}$: $m$번째 문서의 $n$번째 단어를 제외하고, 모든 단어에 대한 토픽을 나타내는 확률 변수

위 식처럼 결합 확률 분포를 직접 구하는 것 대신, 조건부 확률을 통해 샘플을 만들어 낸다. 다시 말하면, Gibbs sampler는 각 잠재 변수의 좋은? 샘플을 만들어 내기 위해서, 그 외 다른 모든 잠재 변수는 현재 값으로 고정시키고 나서 특정 잠재 변수에 대한 조건부 확률을 계산하고 이 조건부 확률 분포로 부터 해당 잠재 변수 값을 샘플링 하게 된다.

샘플링은 inverse transforming sampling 방식으로 구현한다.

결과적으로, 만약 $m$문서의 $n$번째 단어의 토픽이 $v$로 할당된다라고 할 때, 그 확률은 다음과 같이 정리 된다.

$$\begin{aligned} \color{blue} { P(Z_{(m,n)} = v|Z_{-(m,n)}, W;\alpha,\beta) } &\propto P(Z_{(m,n)}=v, Z_{-(m,n)}, W;\alpha, \beta) \\ &\propto ... \\ &\propto \displaystyle\prod_{i=1}^{K} \Gamma \bigg( n_{m,(\cdot)}^{i} + \alpha_{i} \bigg) \displaystyle\prod_{i=1}^{K} \cfrac {\Gamma(n_{(\cdot), v}^i)+\beta_{v}} {\Gamma(\sum_{r=1}^{V} n_{(\cdot),r}^{i} + \beta_{r})} \\ &\propto ... \\ &\propto \color{blue} { \bigg( n_{m,(\cdot)}^{k,-(m,n)} + \alpha_{k} \bigg) \cfrac { \Gamma \bigg( n_{(\cdot),v}^{k,-(m,n)} + \beta_{v} \bigg) } {\sum_{r=1}^{V} n_{(\cdot),r}^{k,-(m,n)} + \beta_{r}} } \end{aligned}$$

• $n_{m,(\cdot)}^{k, -(m,n)}$: $m$번째 문서에서 id값이 $k$인 토픽(단, $Z_(m,n)$은 제외, 즉 현재 단어에 어떤 토픽이 할당되는지는 제외)이 할당된 단어(토큰)의 갯수

위 생략된 부분은 위키피디아에 디테일한 과정이 있으니 참고하기 바란다.

Gibss Sampling 과정 요약

LDA 모델 학습에 있어서 가장 중요한 식이 바로 위(파란색)에 유도되었다.

실제 구현 레벨에서 위 식을 이용하는 방법은 다음의 과정을 따르게 된다. (간단히만 설명)

향후 개인적으로 구현한 LDA 모델을 github에 올릴 예정이다.

1. 모든 문서 내, 모든 단어(토큰) 마다 임의의 토픽을 할당한다.
2. 모든 문서, 모든 단어를 하나씩 스캔하면서, 현재 단어에 할당된 토픽을 무효화 하고, 1 부터 K의 토픽 할당 했을 때의 조건부 확률 값(위의 파란색 식)을 계산한다.
3. 2에서 구한 각 토픽 별 확률값을 누적 확률 분포로 표현하고, 이 누적 함수의 역함수를 구한다.
4. 0 부터 1사이의 난수를 위 역함수의 입력으로하여 함수 값을 찾으면 이것이 현재 단어(토큰)의 $Z$ 값이 샘플링 된 것으로 생각할 수 있다.
5. 다음 단어를 스캔하면서 위 2번 부터 다시 반복한다.

위 3번, 4번 과정에서 설명한 부분이 앞서 언급한 inverse transform sampling 방식을 설명한 것인데 이는 별도의 페이지에서 추가로 섦명하도록 하겠다.

결론적으로, 과정을 반복하다보면 우리가 목표로 하는 잠재 변수에 대한 사후 확률 분포, $P(Z|W;\alpha,\beta)$, 가 점점 (데이터를 가장 잘 설명하는) 목표 분포에 수렴하게 되고, Gibbs Sampling에서는 실제 Z의 샘플을 만들었기 때문에, 각 단어에 어떤 토픽을 할당하는 것이 좋은지 에 대한 결과를 얻을 수 있다.

위 그림은 임의로 가져온 그림이긴 한데, 각 점을 $Z$의 configuration을 나타내는 어떤 state라고 이해하면 좋을 것 같다.

사실 개인적으로는 이 과정이 가장 핵심이라고 생각한다. 그 이유는 현재 단어에 어떤 토픽이 할당 되는 것이 가장 그럴듯 할지에 대해 섦명하는 확률이 식 5인데 argmax를 취하여 할당 될 토픽을 결정하는 것이 아닌, 말 그대로 샘플링을 통해서 결정한다라는 부분을 어떻게 받아들여야 할지를 이해하는 것이 중요하기 때문이다. 이러한 방식이 Markov Chain Monte Carlo(MCMC) 메소드 라고 하는 것인데 이 부분에 대한 섦명은 마찬가지로 별도의 페이지에서 설명할 예정이다.

Gibbs Samping은 대표적인 Markov Chain Monte Carlo(MCMC) 알고리즘이다.

위에 설명한 내용을 이해하기 위해서는 상당히 많은 배경지식 필요하기 때문에 상당 부분 설명이 생략 된 부분이 많이 있지만, 나름 핵심적인 사고 과정은 포함되어 있다고 생각한다. 조금씩 시간이 날 때마다 디테일한 부분을 업데이트 하도록 하겠다.